[PL] STLC 的 categorical semantic
categorical semantic 以我目前的了解就是用 category 對語言的各個部分建模以理解其某些方面的語義,這裡要介紹的就是把 STLC 的 context 作為 objects 的方法(也就是 syntactic category)
1. STLC 的 categorical semantic
在 STLC 裡面一個重要的特性是每個 type 都是封閉的,所以我們可以認為其 syntactic category 中可以視 context 為 type 的串列,並且把單個類型看成只有一個綁定的 context 放進 syntactic category 中當 object
1.1. 什麼是 STLC 中的 product?
在 STLC 中 product 的三個規則如下
\[ \frac{ \Gamma \vdash t : A, \Gamma \vdash u : B }{ \Gamma \vdash (t, u) : A \times B } \quad\quad\quad\quad \frac{ \Gamma \vdash t : A \times B }{ \Gamma \vdash \text{fst}(t) : A } \quad\quad\quad\quad \frac{ \Gamma \vdash t : A \times B }{ \Gamma \vdash \text{snd}(t) : B } \]
思考一下就可以發現這是在說

很容易猜到下一步就是 \(A \times B\) 有 morphism 可以到 \(A\) 跟 \(B\) 嗎?顯然分別就是兩個遺忘 substitution
- \((t, u) = t\)
- \((t, u) = u\)
這就說明了,STLC 的 semantic category 中任意兩個 object 的 product 也是 STLC 的 object。而且可以看出 \(\Gamma\) 跟 \(A \times B\) 在 STLC 裡自然的關係,就是 product internalize 了 context,你可以用 \(\Gamma\) 說明有哪些需要填補,才能滿足一個 \(A \times B\) 的構造所需來思考這個連結
1.2. empty context
現在我們要考慮一個奇特的情況,也就是空的 context 的存在
\[ \frac{ \Gamma \vdash A }{ \emptyset, \Gamma \vdash A } \quad\quad\quad \frac{ \Gamma \vdash A }{ \Gamma, \emptyset \vdash A } \]
上面的 \(\Gamma, \emptyset\) 跟 \(\emptyset, \Gamma\) 顯然並無不同,所以在類型裡面應該也要有 empty context \(\emptyset\) 的對應,我們先叫它 \(*\)。根據上面的規則,可以畫出下面這張圖

我們可以更仔細的去看
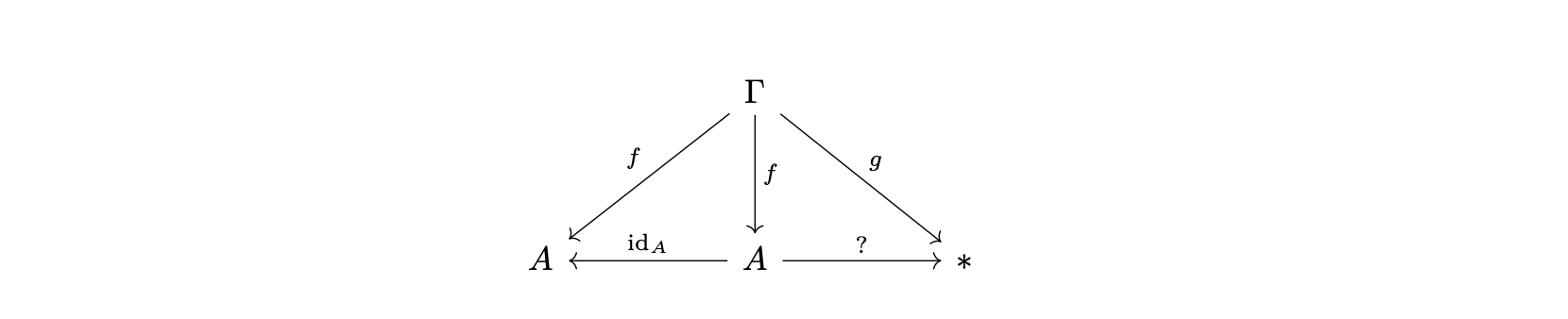
首先可以知道 \(*\) 在左右這張圖都足以處理。接著問題是 \(? \circ f = g\) 嗎?這裡要回歸 \(*\) 是 empty context 來思考,由於這件事是真的,而任何 context 又都是從 empty context 增加任意個 type 與任意排列而成,所以 context 到 empty context 有且只有一個 morphism。這反過來告訴我們 \(*\) is terminal,並且證明 \(? \circ f = g\)
而這也說明 \(A \times * = * \times A = A\),因為 \(A \times *\) 跟上面的交換圖有一樣的構造
這證明了 STLC 的 semantic category 存在 terminal object,事實上我們很常用 \(()\) 表示這個 object
1.3. \(A \to B\) 是什麼?
\[ \frac{ \Gamma, x : A \vdash t : B }{ \Gamma \vdash \lambda x . t : A \to B } \quad\quad\quad\quad\quad\quad\quad \frac{ \Gamma \vdash t : A \to B, \Gamma \vdash u : A }{ \Gamma \vdash \text{app}(t, u) : B } \]
我們逐條翻譯規則到範疇會得到
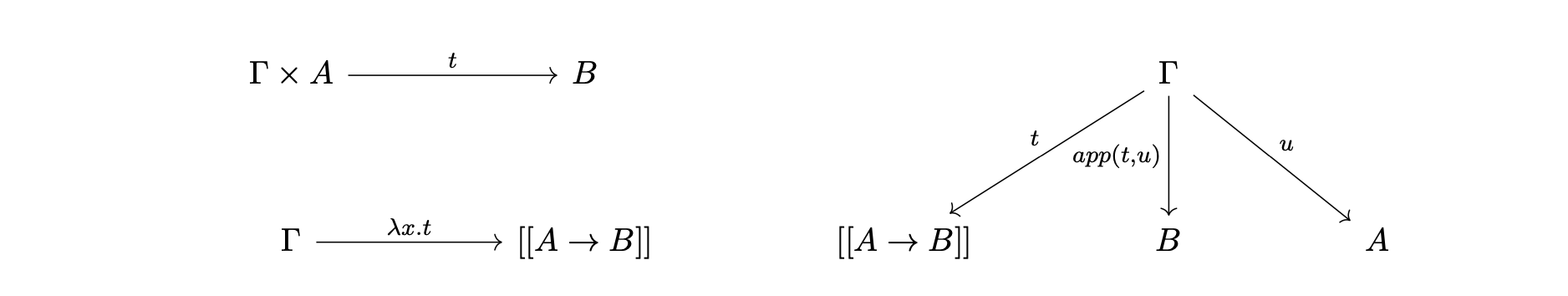
根據 \(\beta\)-reduction,我們知道 \(\text{app}(t,u) = t[x:=u] = t \circ u\)
根據這些,我們可以得知
- 對任意 \(t : \Gamma \times A \to B\) 來說,存在 \(\lambda x.t : \Gamma \to [[A \to B]]\)
- 對任意 \(t : \Gamma \to [[A \to B]]\) 跟 \(u : \Gamma \to A\),可以用 \(app(t,u)\) 組合出 \(\Gamma \to B\)
- 對任意 \(t : \Gamma \times A \to B\) 跟 \(u : \Gamma \to A\),有 \(app(\lambda x.t, u) = t \circ (id_\Gamma,u)\)
\((id_\Gamma,u)\) 的意思是 \(\Gamma\) 只套用 \(u\) 替換而已
根據 \(app\) 的特性,我們應該可以定義
\[ app : [[A \to B]] \times A \to B \]
並且 \(\beta\)-reduction 的屬性可以規定成
\[ app \circ (\lambda x.t, u) = t \circ (id_\Gamma, u) \]
於是我們可以整理出

接著把 \(u\) 換成 \(id_A\) 可以得到

可以直觀的看到這就是 introduction 規則,因為我們有 \(\Gamma \times A\) 可以推出 \(B\) 表示可以用這個 \(t : \Gamma \times A \to B\) 定義 \(\lambda x .t\),事實上這就是 exponential object 的定義

所以可以知道 STLC 還需要對任意兩個 objects 成立 exponential
1.4. 總結
STLC 的 semantic category
- 任意兩個 object 有 product
- 存在 terminal object
- 對任意兩個 objects 成立 exponential
還有一個 category 就長這樣,叫做 Cartesian Closed Category (簡稱 CCC)
所以 STLC 的 syntactic category 可以用 CCC 來研究
2. 結語
知道這些抽象方式之後,我們就可以用一些已知的關係來研究。比如利用 CCC 中的同構 \((X ^ Y) ^ Z \cong (X ^ Z) ^ Y\),所以可以知道 STLC 參數順序可以調換而不改變運算。下次希望可以弄懂 monad 推導的流程